
Hypothesis Testing
There are several main types of hypothesis testing, each suited to analyzing different kinds of data and research questions. Here’s a breakdown of some common types:
Parametric Tests:
- These tests rely on the assumption that the data follows a specific probability distribution (like normal distribution).
- Z-test: Used to compare the mean of one sample to a known value or compare the means of two independent groups when the sample sizes are small, and the population standard deviations are known to be equal.
- T-test: Similar to a z-test but used when the population standard deviation is unknown, or the sample sizes are small (often used with estimates from the data itself). There are different variations of t-tests for different scenarios (e.g., one-tailed vs. two-tailed, paired vs. independent samples).
- ANOVA (Analysis of Variance): Compares the means of more than two groups and helps determine if there’s a significant difference between them.
Non-Parametric Tests:
- These tests make fewer assumptions about the underlying data distribution and can be used with non-normal data or ordinal data (ranked data).
- Examples:
- Chi-Square Test: Used to assess the relationship between two categorical variables or test if observed frequencies differ significantly from expected frequencies in a single categorical variable.
- Mann-Whitney U Test: Compares the medians of two independent groups and is a non-parametric alternative to the two-tailed t-test.
- Wilcoxon Signed-Rank Test: Compares the medians of two related samples (paired data) and is a non-parametric alternative to the paired t-test.
Choosing the Right Test:
The type of hypothesis test you choose depends on your specific research question and data characteristics:
- Data Type: Consider if your data is continuous (e.g., height, weight) or categorical (e.g., hair color, job category).
- Sample Size: Some tests, like z-tests, have specific assumptions about sample size.
- Number of Groups: Are you comparing two groups, multiple groups, or a single sample to a known value?
- Normality: Is your data normally distributed, or is it skewed or non-normal?
Statistical Tests
| Test | Purpose | Data Type | Calculation (Basic) | Assumptions |
|---|---|---|---|---|
| Z-Test | Compares a single sample mean to a known population mean | Continuous, normally distributed | 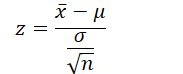 | Population standard deviation (σ\sigmaσ) known, normality |
| T-Test (Independent Samples) | Compares the means of two independent groups | Continuous, normally distributed (or large samples) | 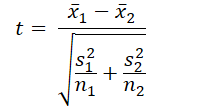 | Normality (or large samples), equal variances |
| T-Test (Paired Samples) | Compares the means of two related samples (paired data) | Continuous, normally distributed (or large samples) | 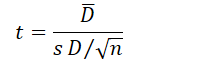 | Normality (or large samples) |
| ANOVA (One-Way) | Compares the means of more than two independent groups | Continuous, normally distributed (or large samples) | Uses Sum of Squares (SS) & Mean Squares (MS) to compare variance between groups and within groups | Normality (or large samples), equal variances, independence |
| Chi-Square Test (Goodness-of-Fit) | Tests if observed frequencies match expected frequencies in one or more categories | Categorical | 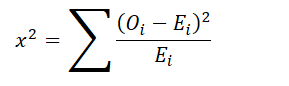 | Independence of observations, minimum expected frequency |
| Chi-Square Test (Independence) | Tests if two categorical variables are independent | Categorical | 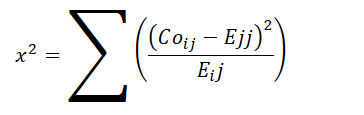 | Independence of observations, minimum expected frequency |
| Mann-Whitney U Test | Compares the medians of two independent groups (non-parametric) | Ordinal or continuous | Uses ranking and calculation of U statistic | No assumptions about normality or equal variances |
| Wilcoxon Signed-Rank Test | Compares the medians of two paired samples (non-parametric) | Ordinal or continuous | Uses ranking of differences between paired samples and calculation of T statistic | No assumptions about normality |
We hope you found the information helpful! If you learned something valuable, consider sharing it with your friends, family, and social networks.
Also Read:
- Wilcoxon Signed-Rank Test Explained
- Mann-Whitney U Test Explained
- Chi-Square Test Explained
- ANOVA Analysis of Variance Explained
- T-Test Explained
- Z-Test Explained
Hi, I am Vishal Jaiswal, I have about a decade of experience of working in MNCs like Genpact, Savista, Ingenious. Currently i am working in EXL as a senior quality analyst. Using my writing skills i want to share the experience i have gained and help as many as i can.
