What is a Hypothesis?
A hypothesis is an educated guess or a tentative statement about a phenomenon that can be tested through research. It serves as a foundation for an investigation, guiding researchers in collecting and analyzing data. A good hypothesis is testable, falsifiable and specific. An example of a good hypothesis may be, imagine you observe that plants seem to grow taller when exposed to sunlight. You might formulate a hypothesis like: “Plants exposed to more sunlight will grow taller than plants with less sunlight exposure.”
What is a Statistical Hypothesis?
A statistical hypothesis is a specific statement about a population parameter that can be tested using data collected from a sample. It is a formal way of phrasing a prediction or making a claim within the framework of statistical analysis.
Components of a Statistical Hypothesis: It is my observation that in order for a hypothesis to be a good hypothesis it has to have two components.
- Population Parameter: A good hypothesis refers to a characteristic of the entire population for example, population mean or proportion.
- Specific Claim: A good statistical hypothesis makes a specific statement about the value of the population parameter.
What are the types of Statistical Hypotheses?
There are two main types of statistical hypotheses which are used in hypothesis testing.
Null Hypothesis (H₀): Null Hypothesis represents the default assumption, often stating that there is “no effect” or “difference” between groups. It serves as the baseline for comparison between the groups. Null hypotheses usually include phrases like “no effect,” “no difference,” or “no relationship.” In mathematical terms, they always include an equality sign like =, ≥ or ≤. The null hypothesis is always status quo.
Alternative Hypothesis (H₁): An alternative hypothesis reflects the actual claim or prediction you are interested in testing. It states the opposite of null hypothesis, indicating that there “is an effect” or “there is a difference” between the groups, in other words this It is the claim that you expect, or hope will be true. In mathematical terms, they always include signs like ≠, > or <.
Example: If you want to investigate if a new fertilizer increases plant growth. Here is what the hypotheses might look like:
- Null Hypothesis (H₀): There is no difference in average plant height between plants using the new fertilizer and those using the standard fertilizer (average height in both groups is equal).
- Alternative Hypothesis (H₁): Plants using the new fertilizer will have a greater average height compared to plants using the standard fertilizer.
What are the similarities between the Null and Alternative hypothesis?
While the Null and Alternative hypothesis play opposite roles in hypothesis testing, yet there are a few similarities.
| Feature | Description |
|---|---|
| Focus on Population | Both hypotheses are statements about a characteristic of the entire population you’re studying, not specific sample data points. |
| Sample Data Evaluation | Neither hypothesis is directly tested on the entire population. Instead, sample data is used to assess the plausibility of each based on statistical methods. |
| Testing Framework | Formulating both null and alternative hypotheses is crucial for setting up the statistical testing process. |
What are the differences between the Null and Alternative hypothesis?
| Feature | Null Hypothesis (H₀) | Alternative Hypothesis (H₁) |
|---|---|---|
| Focus | No effect or No difference | Effect exists or Difference exists |
| Example (Plant Growth) | There is no difference in average plant height between fertilized and unfertilized groups. | Plants with fertilizer will have a greater average height compared to unfertilized plants. |
| Role | Default assumption, Baseline for comparison | Specific claim being investigated |
| Decision Making | Supported if evidence is inconclusive | Tentatively supported if evidence rejects H₀ |
| Direction | Two-tailed (no specific direction of effect) | One-tailed (predicts a specific direction of effect – greater than, less than) or Two-tailed (predicts an effect in either direction) |
| Burden of Proof | No burden of proof (assumed true until evidence suggests otherwise) | Burden of proof to show H₀ is false |
| Wording | Often uses phrases like “no effect,” “is equal to,” or “no difference” | Often uses phrases like “greater than,” “less than,” “not equal to,” or “different” |
| Symbols | Uses equality symbol (=) | Uses inequality symbol (≠, <, or >) depending on the alternative hypothesis (one-tailed or two-tailed) |
| Decision Rule (using significance level α) | p ≤ α | Rejected (evidence suggests H₀ is false) |
| Decision Rule (using significance level α) | p > α | Failed to reject H₀ (insufficient evidence to reject null hypothesis) |
What are Type I and Type II Errors in Hypothesis Testing?
Null Hypothesis
| True | False | |
| Reject | Type I Error (α) | No Error |
| Accept | No Error | Type II Error (β) |
- When Null Hypothesis is true and we reject the null hypothesis, we commit Type I error. for example,
- Ho – Earth is not flat.
- Ha – Earth is flat.
- In this case Null Hypothesis is true but we reject it, so we are committing Type I error.
- If we accept the null hypothesis, we do not commit any error.
- When Null Hypothesis is False and we accept it, we commit Type II error, for example,
- Ho – A new drug has no effect on a disease.
- H1 – A new drug has effect on a disease.
- In this case Null hypothesis is False and we reject the null hypothesis we do not commit any error.
- If we accept the Null Hypothesis, we will be committing Type II error.
What are the key metrics in Hypothesis Testing? Significance, Confidence, and Power
- Significance Level: The threshold for deciding whether to reject the null hypothesis. A common significance level is 5% (α = 0.05), meaning there is a 5% risk of committing a Type I error.
- Confidence Level (1 – α): The probability of correctly accepting the null hypothesis when it is true. A confidence level of 95% (1 – α = 0.95) is considered good, indicating a high degree of certainty in the test results.
- Power of the Test (1 – β): The probability of correctly rejecting the null hypothesis when it is false. A higher power indicates a better ability of the test to detect an effect when there is one.
What is Z critical?
Z critical (z*) refers to a specific value on the standard normal distribution that corresponds to a chosen significance level (alpha, α) in hypothesis testing. It represents the cutoff point, beyond which we would reject the null hypothesis.
Z critical is a value used in Z tests to determine whether to reject or fail to reject the null hypothesis, Based on calculated z-statistic (z score) from sample data.
What is One-tailed and Two-tailed test?
A One tailed test is the test where critical region to reject the null hypothesis is eighter on extreme left or right side of the mean, A two tailed test is the test where critical region to reject the null hypothesis is on both side of the mean.
What are the steps to conduct a hypothesis testing?
Steps in Hypothesis Testing
- Formulate Hypotheses
- Select Significance Level (α)
- Choose the Appropriate Test and Calculate the Test Statistic
- Determine the Critical Value and Decision Rule
- Make a Decision
- Draw a Conclusion
Example Scenario:
You want to test whether a new teaching method improves the pass rate of students compared to the traditional method.
Step-by-Step:
Formulate Hypotheses:
H₀: The pass rate with the new method is equal to the pass rate with the traditional method.
H₁: The pass rate with the new method is higher than the pass rate with the traditional method.
Select Significance Level:
Choose α = 0.05.
Choose the Test and Calculate the Test Statistic:
Use a z-test for proportions.
Calculate the test statistic using sample proportions.
Determine Critical Value and Decision Rule:
Find the critical z-value for a one-tailed test at α = 0.05.
Make a Decision:
Compare the calculated z-value to the critical z-value.
Draw a Conclusion:
If the z-value is greater than the critical value, reject H₀ and conclude that the new teaching method improves the pass rate.
Example:
A shopkeeper is selling cashews of 100gm packets, a customer complains that the actual weight of the packet is less than 100 gms, the shopkeeper takes a sample of 49 packets, and determines that the average weight of the packet is 95 gms. The packets vary 5 gms.
Ho : weight = 100gms
Ha : weight < 100gms
Significance level for the test would be 5 %
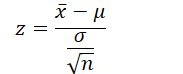
n = 49, X̄ = 95, μ = 100, σ = 5
Zs = 
= -7
Zc = -1.64
Because Z critical lies farther away from z score on normal distribution which tells us that the null hypothesis is correct.
Watch this video to understand the calculation.
We hope you found the information helpful! If you learned something valuable, consider sharing it with your friends, family, and social networks.
Reference: Khan Academy, Wikipedia
Also Read: