T-Test: Overview and Requirements
- T-test: Similar to a z-test, but used when the population standard deviation is unknown or the sample sizes are small (often used with estimates from the data itself). There are different variations of t-tests for different scenarios (e.g., one-tailed vs. two-tailed, paired vs. independent samples).
- One-Sample T-Test: Compares the mean of a single sample to a known value (often the population mean).
- Independent Samples T-Test: Compares the means of two independent groups.
- Paired Samples T-Test: Compares means from the same group at different times (e.g., before and after a treatment).
Requirements to Perform a T-Test
Essential Requirements:
- Sample Size (Ideally):
- While t-tests can be used with small sample sizes, it is generally recommended to have a minimum sample size of 30 for each group to ensure the Central Limit Theorem applies, which helps in approximating the normality of the sample distribution.
- Independence (for Two Groups):
- The samples must be independent. This means the selection of a data point from one group should not influence the selection of a data point from the other group. Random sampling techniques are crucial to maintain independence.
Additional Considerations:
- Normality of Data (Assumption):
- The t-test assumes that the data follows a normal distribution. However, the t-test is robust to violations of normality, especially with larger sample sizes. For smaller sample sizes, if the data significantly deviates from normality, consider data transformations (e.g., log transformation) or non-parametric tests (e.g., Mann-Whitney U test).
- Homogeneity of Variance (Optional but Important):
- This assumption refers to the equality of variances between the two groups being compared. While not strictly necessary for all t-tests, unequal variances can affect the accuracy of the test. Levene’s test can be used to check for homogeneity of variance. If the variances are unequal, you can use Welch’s t-test, which adjusts for this issue.
Key Differences from Z-Test Requirements:
- Unknown Population Standard Deviation (σ):
- Unlike the z-test, which requires a known population standard deviation, the t-test can be used when σ is unknown. The t-test estimates the standard deviation from the sample data itself, making it more flexible.
- Variations of T-Test:
- The t-test has different versions to address specific scenarios:
- One-tailed vs. Two-tailed Tests: Depending on whether you are testing for a specific direction of the effect (one-tailed) or any direction (two-tailed).
- Paired vs. Independent Samples: Paired t-tests are used for comparing means from the same group at different times, while independent t-tests compare means from two different groups.
- Equal vs. Unequal Variances: Different formulas and considerations are used based on whether the variances are assumed to be equal or unequal.
- The t-test has different versions to address specific scenarios:
Steps to Perform a T-Test:
- Formulate Hypotheses:
- Null Hypothesis (H₀): Assumes no difference between the groups.
- Alternative Hypothesis (H₁): Assumes a difference exists.
- Choose the Type of T-Test:
- Decide if you need a one-sample, independent samples, or paired samples t-test based on your data and research question.
- Calculate the Test Statistic (t-score):
- Use the appropriate formula based on the type of t-test:
- For one-sample t-test:
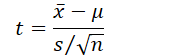
- For independent samples t-test:
-
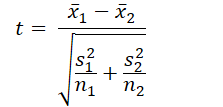
- For paired samples t-test:
-
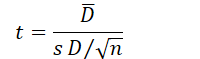
- Use the appropriate formula based on the type of t-test:
- Determine Degrees of Freedom (df):
- For one-sample t-test: 𝑑𝑓=𝑛−1
- For independent samples t-test: 𝑑𝑓=𝑛1+𝑛2−2
- For paired samples t-test: 𝑑𝑓=𝑛−1
- Choose Significance Level (α):
- Common choices are 0.05 (5%) or 0.01 (1%).
- Compare t-Score to Critical Value:
- Use a t-distribution table or software to find the critical t-value based on your chosen α and degrees of freedom.
- Reject H₀ if the absolute value of the t-score is greater than the critical t-value.
- Draw a Conclusion:
- Based on the comparison, either reject or fail to reject the null hypothesis.
Example Calculation: Independent Samples T-Test
Scenario: We want to compare the average height of male and female students in a university. We randomly select 20 male students and measure their heights, and do the same for 25 female students.
Data:
| Gender | Sample Size (n) | Mean Height (cm) | Standard Deviation (s) |
|---|---|---|---|
| Male | 20 | 175 | 5 |
| Female | 25 | 168 | 4 |
Steps:
- Formulate Hypotheses:
- Null Hypothesis (H₀): There is no significant difference in the average height of male and female students (μ_male = μ_female).
- Alternative Hypothesis (H₁): There is a significant difference in the average height of male and female students (μ_male ≠ μ_female).
- Choose the Type of T-Test:
- We need an independent samples t-test because we are comparing two independent groups (male and female students).
- Calculate the Test Statistic (t-score):
- Use the formula for independent samples t-test:
- Where:
- x̄₁: Mean height of males (175 cm)
- x̄₂: Mean height of females (168 cm)
- s₁: Standard deviation of males (5 cm)
- s₂: Standard deviation of females (4 cm)
- n₁: Sample size of males (20)
- n₂: Sample size of females (25)
- Calculate the t-score:
- Determine Degrees of Freedom (df):
- df = n₁ + n₂ – 2 = 20 + 25 – 2 = 43
- Choose Significance Level (α):
- Let’s use α = 0.05 (5%) as a common significance level.
- Compare t-Score to Critical Value:
- Using a t-distribution table with df = 43 and α = 0.05, the critical t-value is approximately 2.004.
- Our calculated t-score (1.41) is less than the critical t-value (2.004).
- Draw a Conclusion:
- Since the absolute value of the t-score (1.41) is less than the critical t-value (2.004), we fail to reject the null hypothesis (H₀).
- This suggests that there is not enough evidence to conclude that there is a statistically significant difference in the average height of male and female students in this sample.
Note: This is a simplified example. Real-world scenarios would likely use statistical software for more precise calculations and p-value analysis.
We hope you found the information helpful! If you learned something valuable, consider sharing it with your friends, family, and social networks.
Also Read: